The Physics of Baseball
Alan M. Nathan
University of Illinois

Baseball Papers of Alan Nathan

1. Dynamics of the Baseball-Bat Collision,

   Alan M. Nathan, American Journal of Physics 68, 979-990 (2000).

   

   The moment of impact
   Courtesy, Champaign News-Gazette

   This paper develops a dynamic model for wooden bats, taking into account their vibrational properties. The model is then used to describe the collision between bat and ball. Based on the preliminary version of this paper, Jeremy Manier wrote an article Science has a Sweet Spot for Baseball that appeared in the April 3, 2000 issue of the Chicago Tribune (front page, above the fold!), which features an interview with me about the bat-ball collision.




2. Characterizing the Performance of Baseball Bats,

   Alan M. Nathan, American Journal of Physics 71, 134-143 (2003).

   

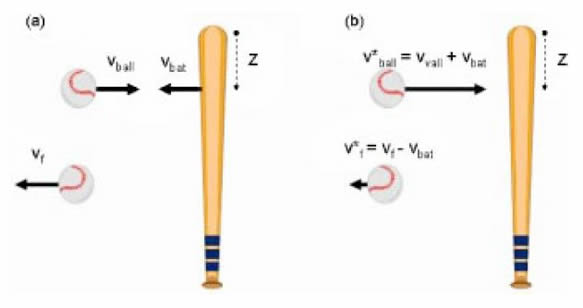   schematic of the baseball-bat collision in the
   (a) usual field frame and the (b) bat rest frame.

   This article defines a set of laboratory measurements that can be performed on a bat and then used to predict performance in the field. Using a computational model, it is shown that bat performance depends on the interplay of the elasticity of the ball-bat collision, the inertial properties of the ball and bat, and the bat swing speed. This paper is the foundation for modern efforts to regolate the performance of non-wood bats.

3. Scattering of a Baseball by a Bat,

   Rod Cross and Alan M. Nathan, American Journal of Physics 74, 896-904 (2006).

   This paper reports on an experiment to study the spin resulting from a low-speed ball-bat collision. The data are relevant for determining whether a hit curveball has more backspin than a hit fastball. Click here to see a short video clip of the experiment in action. That handsome fellow holding the bat is Rod.

4. Experimental Study of the Gear Effect in Ball Collisions,

   Rod Cross and Alan M. Nathan, American Journal of Physics 75, 658-664 (2007).

5. Effect of Spin on the Flight of a Baseball,

   Alan M. Nathan, American Journal of Physics 76, 199-224 (2008).

   

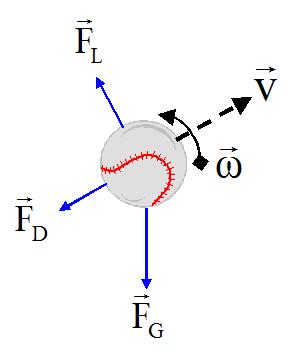   Forces on a baseball in flight.

   In this paper I report on an experiment to measure the quantitative effect of spin on the flight of a baseball. This topic has relevance for the movement of pitched baseballs as well as on the trajectory of a batted baseball.

   1. A talk based on this work was presented at the IMAC XXIV Meeting of the Society of Experimental Mechanics, January 30, 2006.
   2. A presentation based on this work entitled "Baseball aerodynamics: What do we know and how do we know it?" was presented at the SABR36 convention in Seattle (June 2006).
   3. A presentation based on this work entitled "The Flight of a Baseball" was presented at the March 2010 APS meeting.

6. Paradoxical Pop-ups: Why are They Difficolt to Catch?,

   Michael. K. McBeath, Alan M. Nathan, A. Terry Bahill, and David G. Baldwin, American Journal of Physics 76, 723-729 (2008).

   

   Example of a paradoxical popup.

   This paper examines the unusual trajectories of towering popups with lots of backspin. It is shown that the normal strategy used by outfielders to intercept fly balls leads to systematic vacillation in running paths for these popups. One example is shown in the animation. For another example, take a look at this video taken from a Red Sox vs. Tampa Bay game on September 15, 2008. Note the third baseman Kevin Cash (normally a catcher) overruns the ball, which initially was headed toward the seats along the third baseline but then veers back towards the field. This is the quintessential paradoxical popup, indicative of a lot of backspin on the ball. Note also what happens to the ball when it hits the ground. The backwards bounce is further indication of large amount of backspin on the ball.

7. Performance Versus Moment of Inertia of Sporting Instruments,

   Rod Cross and Alan M. Nathan, Sports Technology 2, 7-15 (2009).

   by Rod Cross and myself (Sports Technology, vol. 2, pp 7-15, 2009). It is shown that for a given coefficient of restitution (COR), both the intrinsic power and the swing speed of a tennis racquet or baseball bat correlate strongly with the MOI about an axis through the handle and only weakly with the mass.

8. A Determination of the Dynamic Response of Softballs,

   Lloyd V. Smith, Alan M. Nathan, and Joseph G. Duris, Sports Engineering 12, 163-169 (2010).

9. Corked Bats, Juiced Balls, and Humidors: The Physics of Cheating in Baseball,

   Alan M. Nathan, Lloyd V. Smith, Warren L. Faber, and Daniel A. Russell, American Journal of Physics 79, 575-580 (2011).

   Three questions of relevance to Major League Baseball are investigated from a physics perspective. Can a baseball be hit farther with a corked bat? Is there evidence that the baseball is more lively today than in earlier years? Can storing baseballs in a temperature- or humidity-controlled environment significantly affect home run production? These questions are subjected to a physics analysis, including an experiment and an interpretation of the data. The answers to the three questions are no, no, and yes. A very nice popularized summary of the paper was written by Chris Solomon and appeared in Smithsonian Magazine in June, 2011.

10. A Comparative Study of Baseball Bat Performance,

    Alan M. Nathan, J. J. Crisco, R. M. Greenwald, D. A. Russell, and Lloyd V. Smith, Sports Engineering 13, 153-162 (2011).

11. Reducing the Effect of the Ball on Bat Performance Measurements,

    Alan M. Nathan, Lloyd V. Smith, and Warren L. Faber, Sports Technology 4, 19-28 (2012).

    A new technique is described to normalize the performance of a bat to the coefficient of restitution and stiffness of the baseball or softball used to measure the performance. The technique is developed theoretically and tested experimentally. It is shown to be vastly superior to a different normalization technique that has been popolarly used.

12. Simplified Models for the Drag Coefficient of a Pitched Baseball,

    David Kagan and Alan M. Nathan, The Physics Teacher 52, 278-280 (2014).

    Techniques are described to determine the drag coefficient from PITCHf/x data. These techniques shoold be suitable for classroom instruction in introductory physics courses.

13. Statcast and the Trajectory Calculator,

    David Kagan and Alan M. Nathan, The Physics Teacher, 55, 134-136 (2017).

    A tool is presented for calculating trajectories of baseballs and used to analyze a home run hits by Alex Rodriquez in 2015.

14. Oblique Collisions of Baseballs or Softballs with a Bat,

    Jeffrey R. Kensrud, Alan M. Nathan, and Lloyd V. Smith, American Journal of Physics, 85, 503-509 (2017).

    Oblique impacts of a swinging bat with a stationary ball are performed and the resulting velocity and spin of the batted ball are measured. The results are analyzed in the context of a ball-bat collision model and the parameters of that model are determined.

1. A Study of Softball Player Swing Speed,

   Lloyd Smith, Jeff Broker, and Alan Nathan, Sports Dynamics Discovery and Applications, eds. A. Subic, P. Trivailo, and F. Alam, RMIT University, Melbourne Australia, pp. 12-17 (2003).

   

   This presents the results of a 2002 field study sponsored by the Amateur Softball Association. The data show that the swing speed of a typical player is inversely related to the bat moment of inertia about the handle (with a fixed bat weight) and nearly independent of the weight of the bat (at fixed moment of inertia).

2. The Physics of the Trampoline Effect in Baseball and Softball Bats,

   Alan M. Nathan, Daniel A. Russell, and Lloyd V. Smith, The Engineering of Sport V, eds. M. Hubbard, R. Mehta, and J. Pallis, UC Davis, Davis CA, pp. 38-44 (2004). Proceedings of 5th ISEA Conference, Davis CA, September 2004.

   

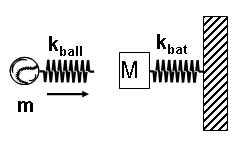   Toy model for the trampoline effect.

   This paper presents a simple physical picture of the "trampoline effect" in hollow bats and demonstrates how the effect leads to a larger coefficient of restitution. A special section presents new data showing there is no measureable trampoline effect with a corked bat. This paper was presented at the September 2004 meeting of the International Sports Engineering Association in Davis, CA.

3. Effect of Ball Properties on the Ball-Bat Coefficient of Restitution,

   A. M. Nathan and L. V. Smith, 4th Asia-Pacific Congress on Sports Technology, Honololu, Hawaii, The Impact of Technology on Sport, 257-262 (2009).

   This paper presents a simple physical model relating the ball-bat coefficient of restitution (BBCOR) to the ball COR and stiffness. Using the model, a technique is developed to normalize the BBCOR to a standard ball. This paper will be presented at the 4th Asia-Pacific Congress on Sports Technology (APCST2009) in September 2009 and was published in the proceedings.

4. Analysis of Knuckleball Trajectories,

   Alan M. Nathan, Procedia Engineering 34, 116-121 (2012). Proceedings of 9th ISEA Conference, Lowell MA, Joly 2012.

   An analysis of knuckleball trajectories is presented using data from the PITCHf/x video tracking system for pitches thrown in actual MLB games. The data reveal that, contrary to popolar belief, knuckleball trajectories are as smooth as those from normal pitches. However, the data also show that the deflection of a knuckleball from a straight-line trajectory is essentially random in both magnitude and direction.

5. Spin of a Batted Baseball,

   Alan M. Nathan, Jonas Cantakos, Russ Kesman, Biju Mathew, and Wes Lukash, Procedia Engineering 34, 182-187 (2012). Proceedings of 9th ISEA Conference, Lowell MA, Joly 2012.

   Experiments are conducted to investigate the spin of a baseball undergoing an oblique collision with a bat. A baseball was fired horizontally at speeds up to 120 mph onto a 3"-diameter cylinder of wood that was rigidly attached to a wall. In one experiment, a two-wheel pitching machine was used in which the backspin or topspin of the incident ball coold be adjusted. In another experiment, an air cannon was used to project the ball with no spin. In both experiments, markers on the ball were tracked with high-speed video to determine the velocity and spin vectors, before and after the scattering. Our primary results are as follows: (1) For a given angle of incidence, the scattered spin is nearly independent of the incident spin; (2) The spin of the scattered baseball is considerably larger than expected for a model whereby the ball rolls before leaving the surface. Implications for the spin of batted baseballs are explored.

6. What New Technologies Are Teaching Us About the Game of Baseball,

   Alan M. Nathan, Proceedings of the EuroMech Physics of Sports Conference, Paris, April 2012 (to be published).

   

   Dependence of fly ball distance on vertical launch angle
   for balls hit in the velocity range shown in the legend.
   These are data from actual MLB games in which the TrackMan
   Doppler radar system was used to measure the fly
   ball trajectory.

   The trajectory of a baseball moving through the air is very different from the one we teach in our introductory classes, in which the only force is that due to gravity. In reality, the aerodynamic drag force (which retards the motion) and the Magnus force on a spinning baseball (which causes the ball to curve) play very important roles that are crucial to many of the subtleties of the game. Despite their importance, our knowledge of how these forces affect the flight of the baseball has been qualitative at best. Recently, however, new tools have been developed for measuring accurate baseball trajectories during an actual game. These tools include both video tracking (the PITCHf/x and related systems) and the TrackMan Doppler radar system. In this article, I will discuss these new tools and give some examples of what they are teaching us about the game of baseball.

7. Relating Baseball Seam Height to Carry Distance,

   Jeffrey R. Kensrud, Lloyd V. Smith, Alan Nathan, and Derek Nevins, Procedia Engineering 112, 406-411 (2015). Proceedings of the 7th Asia-Pacific Congress on Sports Technology APCST 2015.

1. Baseball Pitches,

   A. M. Nathan, Scientific American 277, 102-103 (1997).

2. Bat Performance Standards in NCAA Baseball

   Alan Nathan, Baseball Research Journal 33, 11 (2003)

3. Ball Exit Speed Ratio (BESR)

   James Ashton-Miller, Michael Carroll, Kenneth Johnson, and Alan Nathan, Baseball Research Journal 33, 12-14 (2003)

4. Nickel and Dime Pitches

   Dave Baldwin, Terry Bahill, and Alan Nathan, Baseball Research Journal 35, 25-29 (2006)

5. An Analysis of the Gyroball

   Alan Nathan and Dave Baldwin, Baseball Research Journal 36, 77-80 (2007)

6. The Possible Effect of Steroids on Home-Run Production

   Alan Nathan, Baseball Research Journal 38, 36-38 (2009)

7. Comparing the Performance of Baseball Bats

   Alan M. Nathan, Baseball Analysts, January 18, 2010

8. Home Runs and Humidors: Is There a Connection?

   Alan M. Nathan, Baseball Prospectus, February 25, 2011

9. The Knuckleball Mystique: Using PITCHf/x to Distinguish Perception from Reality

   Alan M. Nathan, Baseball Prospectus, January 31, 2012

10. Dissecting a Mystery Pitch

    Alan M. Nathan, The Hardball Times, January 31, 2012

11. Global Warming and Home Runs: Is There a Connection?

    Alan M. Nathan, Baseball Prospectus, June 5, 2012

12. How Far Did That Fly Ball Travel?

    Alan M. Nathan, Baseball Prospectus, January 8, 2013

13. Is Late Break Real?

    Alan M. Nathan, Baseball Prospectus, March 26, 2013

14. Uncovering the Mysteries of the Knuckleball

    Alan M. Nathan, The Hardball Times Baseball Annual 2014.

15. Testing TrackMan: Just How Well Does TrackMan Work?

    Alan M. Nathan, Lloyd Smith, Jeff Kensrud, Eric Lang, Baseball Prospectus, April 2, 2014

16. The Physics of a Truly Amazing Throw

    Alan M. Nathan, Baseball Prospectus, June 11, 2014

17. How Far Did That Fly Ball Travel? (Redux)

    Alan M. Nathan, Lloyd Smith, Jeff Kensrud, Eric Lang, Baseball Prospectus, December 9, 2014. NOTE: If you are not able to access the Baseball Prospectus article, you read it here.

18. Regulating the Performance of Bats

    Alan M. Nathan, The Hardball Times Baseball Annual 2015.

19. All Spin Is Not Alike

    Alan M. Nathan, Baseball Prospectus, March 31, 2015

20. A Tale of Two Dingers

    Alan M. Nathan, The Hardball Times, April 23, 2015

21. Optimizing the Swing

    Alan M. Nathan, The Hardball Times, November 11, 2015

22. Optimizing the Swing, Part Deux: Paying Homage to Teddy Ballgame

    Alan M. Nathan, The Hardball Times, December 24, 2015

23. Going Deep On Goin' Deep

    Alan M. Nathan, The Hardball Times, April 6, 2016

24. Exit Speed and Home Runs

    Alan M. Nathan, The Hardball Times, July 18, 2016

25. Spinning Out of Control

    Alan M. Nathan, Fangraphs, October 26, 2016

26. Estimating Release Point Using Gameday's New Start_Speed

    Dan Brooks and Alan M. Nathan, Baseball Prospectus, April 5, 2017

27. A Humidor At Chase Field: What's Up With That

    Alan M. Nathan, The Hardball Times, April 17, 2017

28. Fly Ball Carry and the Home Run Surge

    Alan M. Nathan, The Hardball Times, August 24, 2017

29. Pitch Movement, Spin Efficiency, and All That

    Alan M. Nathan, The Hardball Times, August 27, 2018

30. Studies of the Active Spin Ratio

    Charles Young and Alan Nathan, Baseball Prospectus, June 10, 2020.

31. Contributions to Variation in Fly Ball Distance

    Alan Nathan, Fangraphs, July 6, 2020.

32. Exploring the Variation in the Drag Coefficient

    Alan Nathan and Charles Young, Fangraphs, July 31, 2020.

33. Not Just About Magnus Anymore

    Barton Smith, Alan Nathan, and Harry Pavlidis, Baseball Prospectus, November 5, 2020

34. Giancarlo Stanton's Long Single

    Alan Nathan, FanGraphs, October 5, 2021

35. Home Runs and Drag: An Early Look at the 2022 Season

    Jim Albert and Alan Nathan, FanGraphs, May 10, 2022

36. Another Look at the Variation of Drag Coefficients of Baseballs

    Alan Nathan, Baseball Prospectus, May 26, 2022

37. Balls are Traveling Farther in 2024 in Progressive Field

    Jim Albert and Alan Nathan, Baseball Prospectus, June 21, 2024