The Physics of Baseball
Alan M. Nathan
University of Illinois

This paper reports on an experiment to study the spin resulting from a low-speed ball-bat collision. In addition, the formalism for analyzing oblique ball-bat collisions is derived. Click here to see a short video clip of the experiment in action. That handsome fellow holding the bat is Rod.

Experiments are conducted to investigate the spin of a baseball undergoing an oblique collision with a bat. A baseball was fired horizontally at speeds up to 120 mph onto a 3"-diameter cylinder of wood that was rigidly attached to a wall. In one experiment, a two-wheel pitching machine was used in which the backspin or topspin of the incident ball coold be adjusted. In another experiment, an air cannon was used to project the ball with no spin. In both experiments, markers on the ball were tracked with high-speed video to determine the velocity and spin vectors, before and after the scattering. Our primary results are as follows: (1) For a given angle of incidence, the scattered spin is nearly independent of the incident spin; (2) The spin of the scattered baseball is considerably larger than expected for a model whereby the ball rolls before leaving the surface. Implications for the spin of batted baseballs are explored. Click here to see slides of a presentation based on this work.

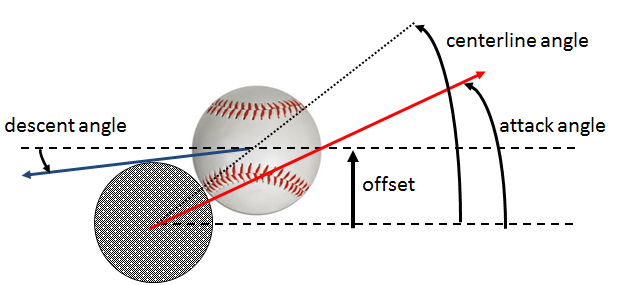
Oblique impacts of a swinging bat with a stationary ball are performed and the resulting velocity and spin of the batted ball are measured. The results are analyzed in the context of a ball-bat collision model and the parameters of that model are determined. The primary results are as follows: (1) The exit velocity is maximized when the attack angle equals the centerline angle ("squared up"); (2) The spin of the batted ball is minimized when the attack angle equals the centerline angle; (3) The launch angle of the batted ball depends primarily on the centerline angle and secondarily on the attack angle.

These are a series of articles that use the formalism developed in the preceding experiments to discuss possible ways for a batter to optimize the swing. The formalism allows one to find exit velocity and launch angle for given attack angle and centerline angle (see picture above). On the other hand, the exit velocity and launch angle are directly related to probability of success, whether it be to hit a home run or to simply get on base. Therefore, we have a direct relationship between parameters of the swing (attack angle and centerline angle) and probability of success.

Color contour plot showing relating exit velocity and launch angle to attack angle and centerline angle. The dashed red line indicates where the attack and centerline angles are equal. The blue curves and colors are exit velocity contours and the black dashed lines are launch angle contours.

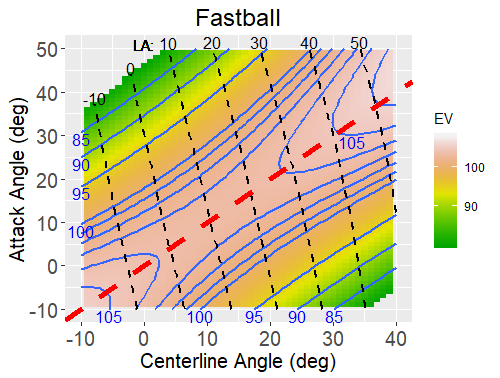
In this presentation (audio link), I present the results of the preceding experiments and show how they are used to predict batted ball parameters from the swing parameters, as shown in the figure. Then I start to address the "reverse engineering" problem, whereby one tries to determine the swing parameters, especially the attack angle, from the batted ball parameters. The issue of timing enters if the attack angle of the bat differs from the descent angle of the ball, and this issue is investigated quantiatively. Finally, the question is addressed whether it is advantageous to alter the swing to sacrifice exit velocity to gain some extra spin on the batted ball.