Dissecting a Mystery Pitch
On April 29, 2011 during the top of the 5th inning of a Toronto at New York game, Yankee pitcher Freddie Garcia threw a split-fingered fastball to the Jay's Juan Rivera. The pitch was captured by the high-speed video camera from the Yankees television broadcast, with sufficient resolution to allow both the spin rate and the rotation axis of the ball to be determined with reasonable precision. Before reading on, you should take a look at the gif below, paying attention to the following details:
- The ball makes a bit over five complete rotations on its sojourn to home plate.
- The rotation axis is such that the rear of the ball, as seen in the video, is turning down and to the left
- The ball has a movement that is down and to the pitcher's left

Gif of the Freddie Garcia splitter, from the YES-MO video..
Juan Rivera swings and misses at Freddie Garcia's splitter. This image is a frame capture from the YES-MO video.
So, does the behavior of this pitch make any sense to you? If you answer NO, then you are among the vast majority of those who have studied this pitch, including both baseball analysts and scientists. So, why is this pitch so unusual? Or, said slightly differently, what would we expect for the movement of the pitch given what we observe about the spin?
So, let's digress for a moment. First, what do we mean by "movement"? Movement is quite simply the deviation of the ball from a straight-line trajectory. For there to be movement, there has to be a force exerted on the ball that is transverse to its direction of motion. For most baseball pitches, there are two sources of transverse force: gravity and the Magnus force. Let's talk about both.
Gravity is the dominant of these forces and is intuitively understood by most of us: It pulls everything downward.
The Magnus force is the aerodynamic force on a spinning baseball. Its magnitude is roughly proportional to the rotation rate of the baseball: the faster it spins, the larger the force. What about the direction? Well, the easiest way to remember the direction of the Magnus force is that it is always in the direction that the leading edge of the ball is turning. The leading edge is the side of the ball seen by the batter.
As an example, a typical four-seam fastball is thrown with backspin, so that the leading edge of the ball is turning up and the Magnus force is upward, opposing gravity. The force of gravity is still larger than the Magnus force, so the net vertical movement is downward but less than it would have been with gravity alone. Likewise, a "12-6" curveball has topspin, so that the leading edge is turning downward; consequently the downward movement is greater than it would have been with gravity alone. A two-seam fastball has it rotation axis oriented slightly differently so that the baseball has a slight sidespin component to it.
In fact, the Garcia pitch, despite being a splitter, is thrown in the two-seam orientation. Since the spin axis it tilted, there is reduced backspin (so that the ball drops more than a typical four-seamer). What about the sidespin? As you can observe from the video, the back of the ball--the side we and the pitcher see--is turning down and to the left. That means the leading edge of the ball--the side seen by the batter--is turning up and to the pitcher's right. That means the expected movement from the Magnus force is up and to the pitcher's right. The fact that it is up is no problem, since we know that gravity will be greater and will pull the pitch down, just as we observe. But the movement to the right is problematic, since that is definitely not what we observe. And that, in a nutshell, is our mystery.
So, what is going on here? Mike Fast posed this question to me in early May, 2011. Mike was the first one to recognize the unusual nature of this pitch and he contacted me to ask whether I had an explanation for it. In turn, I contacted a number of experts in the aerodynamics of sports balls, including my frequent collaborator Professor Rod Cross. And Rod did what really good physicists often do. He came up with some interesting experiments in an attempt to uncover what is going on with our mystery pitch. And I believe he has succeeded. He has written a paper on his findings, "Aerodynamics in the classroom and at the ball park", that has been accepted in American Journal of Physics and will be published in the coming months. He also has a YouTube video,"How to Curve a Baseball or Swing a Cricket Ball", that very nicely demonstrates the physics of what is going on. I highly recommend both the paper and the video. In what follows, I will summarize Rod's findings.
The key to understanding the movement on the Garcia pitch is a phenomenon that is responsible for the movement (in cricket it is called "swing") of the cricket ball, which I will now explain with the help of the following cartoon.
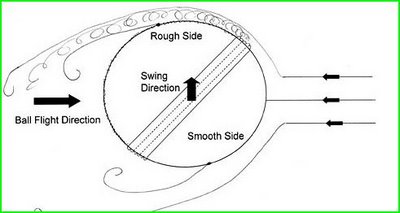
Bird's-eye view depicting the swing of a cricket ball.
Consider air passing over the moving (but for the moment non-spinning, seamless, and smooth) spherical ball. A very thin layer of air (the "boundary layer") actually sticks to the surface of the ball. Because of frictional forces, the air in the boundary layer slows down, stops, and separates from the ball, leaving a low-pressure wake behind the ball. The combination of high pressure in front of the ball due to the oncoming air and low pressure behind it leads to the drag force, which acts opposite to the direction of motion of the ball and slows it down. In this case the boundary layer separation is symmetric with respect to the direction of motion of the ball and there are no transverse forces. For reasons discussed below, the separation point may shift upstream on one side and downstream on the opposite side of the ball. Looking at the ball from the bowler's viewpoint, we see that the separation point at the left side of the ball occurs further downstream than on the right side, resulting in a deflection of the air flow to the right. In effect, the ball exerts a force on the air to the right. Newton's Third Law requires that the air exert an equal and opposite force on the ball, resulting in the swing of the ball to the left.
One way to break the symmetry of the boundary layer separation is to spin the ball. For example, if the ball in the picture were spinning counterclockwise (ignoring for now the seams and the roughness), the ball would pull the boundary layer along with it on the left side of the ball and push against it on the right side, resulting in separation occuring further downstream on the left than on the right. The resulting leftward force on the ball is the conventional Magnus effect. Another way to break the symmetry occurs if there is an asymmetry in the surface roughness of the ball. Again consider the cricket ball in the figure and let us suppose that the ball is perfectly smooth except for the raised seam. Because of the orientation of the seam relative to the air flow, the left surface of the ball is rougher than the right surface. When air flows over a rough patch, such as a seam, the character of the flow changes from smooth ("laminar") to turbulent. The experts--and I am not one of them--say that when the boundary layer air is turbulent, it mixes with high speed air adjacent to it, thereby increasing the average air speed in the boundary layer. The net result is that the air takes longer to separate from the surface. Therefore the boundary layer separation is delayed on the left side, resulting in a deflection of the air flow to the right and a corresponding deflection of the ball to the left. That force is responsible for the conventional swing of a cricket ball. In fact, a cricket bowler typically spins the ball about the equatorial seam, so that the orientation of the seam relative to the motion does not change as the ball rotates.
For a baseball, things are a bit more complicated because of the "figure 8" seam pattern on the ball. Nevertheless, the same essential physics applies. Spinning balls have a Magnus effect. And an asymmetry in the surface roughness can result in transverse forces. The most common example of the latter is the knuckleball. Since the ball is thrown with little or no spin, it is possible to orient the seams to produce an asymmetry in the roughness of the ball that persists throughout the trajectory. If the ball is spinning rapidly, as it is for most "normal" pitches, then conventional wisdom is that the effect of the seams is averaged out during the flight, resulting in no net transverse force. But conventional wisdom is not always right, as we shall see shortly.
Everything I just explained has been known for a long time. What is new are the very clever expereriments of Rod Cross, as explained in his paper. I won't discuss all his experiments but only the one relevant to the Garcia pitch. Cross's clever idea is to investigate the effect of seams on a polystyrene ball, with approximately the same size as a baseball but much lighter. With the same size and seam pattern, the aerodynamic forces will be about the same as on a normal baseball. However, since the polystyrene ball is much lighter than a baseball, the deflection of the ball due to the forces will be larger and much easier to measure. A sketch of the ball and seam pattern through one revolution is shown in the figure below, which I have taken directly from Cross's paper (Fig. 11).
Seam orientation during one revolution for one of Cross's experiments. The ball is shown from the catcher's viewpoint and the spin axis is horizontal (backspin) and tilted slightly in the forward direction. Note the white patch shown by the dotted line on the left side of the ball that persists through one revolution. Thanks to Rod Cross for permission to use his picture.
The ball is moving in a direction that is out of the plane of the page (catcher's view) and is spinning about a horizontal axis (backspin), with the axis tilted slightly forward (i.e., there is a small "gyro" component to the spin). The figure shows clearly that there is a smooth white patch on the left-hand-side of the ball that persists through a complete revolution. Therefore, averaged over one revolution, the left side of the ball is smoother than the right side. The expectation is that the boundary layer separation will be shifted downstream on the right side, resulting in a side force to the catcher's right. That is exactly what Cross sees in his experiment.
Now let's return to the Garcia pitch. If you play back the video one frame at a time, you will see that the upper left quadrant of the ball maintains a white patch throughout the trajectory. A frame grab from the video is shown below, with a red oval indicating the persistent white patch. The spin axis must therefore pass roughly through the middle of the white patch (the "North Pole" of the ball). It must also happen that the spin axis passes through another white patch diametrically opposite (the "South Pole"). We can't see it on the video because it is on the side of the ball facing the catcher, who sees the white patch appears in the lower left quadrant. Therefore, the oncoming air "sees" a left-right asymmetry in the average roughness of the ball. The left side (with the white patch) is smoother than the right side (with the seams). By analogy with the swing of the cricket ball, the movement on the pitch should be to the catcher's right, which is exactly what actually happens. At least qualitatively, the mystery is solved.
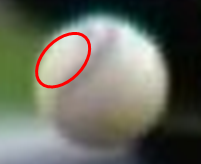
Frame grab of the Garcia pitch, with the red oval indicating the location of the white patch.
It is interestsing to use the PITCHf/x trajectory to estimate the size of the various forces on the ball. The ball was released at 80.1 mph. All three components of acceleration are determined from the standard fit to the trajectory. By counting revolutions, I estimate the ball is rotating at the rate of 800 rpm. From that, I can use the experimental relationship between the rotation rate and the Magnus force to estimate the magnitude of the latter. Since the movement is determined from the components of acceleration and since the Magnus contribution can be estimated, the additional acceleration due to the roughness asymmetry can also be estimated. Here is what I find for the forces, all normalized to the weight of the ball:
- gravity = 1.00
- drag = 0.78
- Magnus = 0.32
- roughness = 0.63
Finally, let me remark that another way to have an asymmetry in the surface roughness is to scuff the ball and arrange for the spin axis to pass through the center of the scuff. Then the side of the ball with the scuff always has the same orientation relative to the air flow, resulting in an asymmetry in the roughness. Which way the ball deflects will depend on the relative importance of the scuff and the seams. If rotating the ball rapidly results in no net asymmetry due to the seams (the "conventional wisdom" referred to earlier), then the ball will deflect in the direction of the scuff.
Thanks to Mike Fast, who first brought this pitch to my attention; to Ed Frank for some helpful suggestions; and to Rod Cross for lots of interesting discussion and for giving me permission to show his work here.
Back to The Physics of Baseball



